Fundamentals of Engineering Design
s
= the density of the sediment; and
= the density of water.
If Eq. (5.29) and Eqs. (5.30a and b) are combined a simplified Meyer-Peter and Mller bedload transport
equation is given as:
qbv
3/2
' 8(J( & J( c)
(5.31)
3
(G&1)gDs
where qbv is the unit channel width bedload transport in volume per time. The term * is known as the
Shields parameter, which represents a dimensionless value of shear stress on the bed material. The Shields
parameter is given by definition as:
J
J( '
(5.32)
((G & 1)Ds
The term *c is the critical Shields parameter. The critical Shields parameter is a threshold value of
dimensionless shear stress where incipient motion exists. Often when working with gravel bed rivers
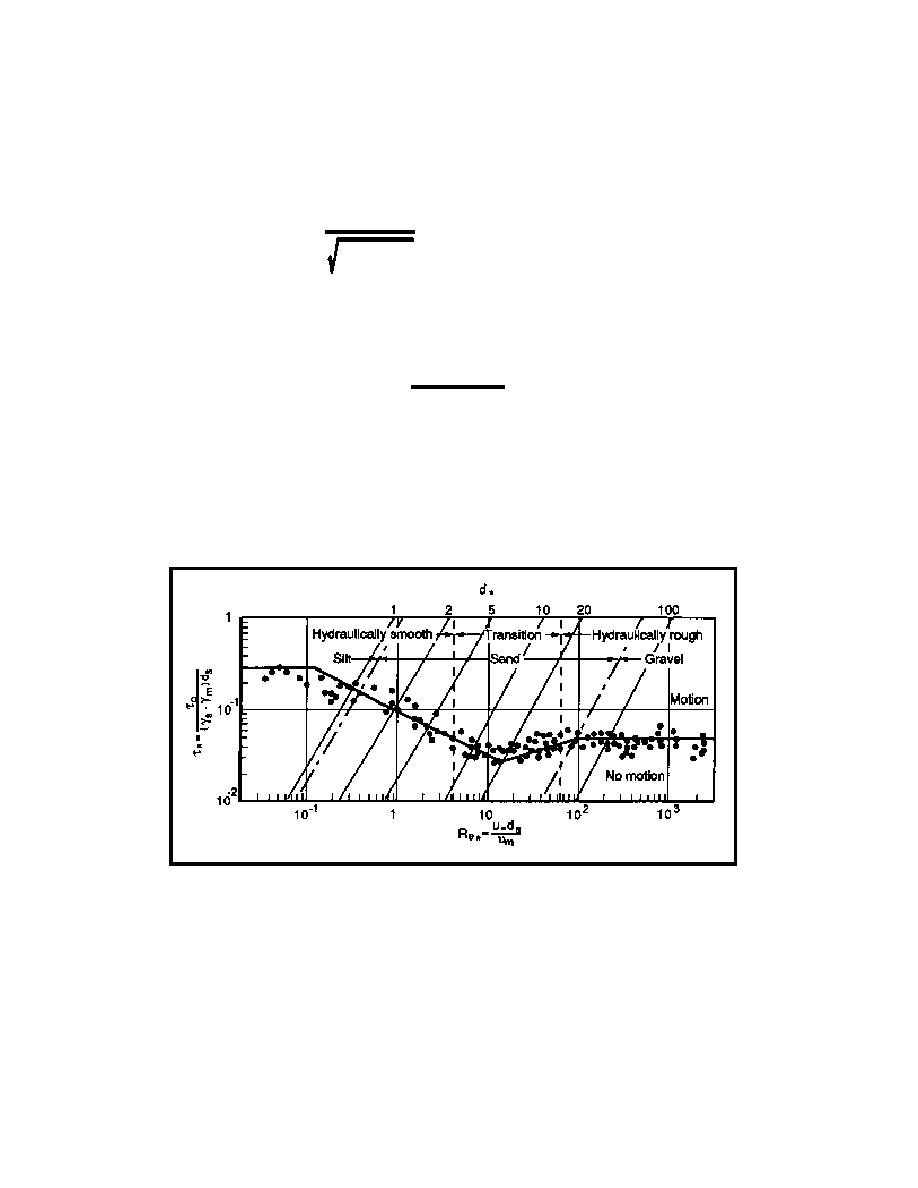
*c = 0.047 is used. A more precise value can be determined using the modified Shields diagram, given
in Figure 5.45, where *c is the value selected from the regression line. However, the Shields diagram was
developed using primarily uniform particle sizes, ignoring the effects of particle hiding and particle exposure.
Figure 5.45 Threshold of Motion for Granular Material (from Julien, 1995)
For well-graded bed sediment or fine gravel, there may be enough material being transported in
suspension that it is necessary to use a total load equation. Julien (1995) presents a plot showing the ratio
of suspended load to total load versus u*/ , where is the particle fall velocity. It can be seen in Figure
5.46 that bedload is the dominant means of sediment transport for values of u*/ less than about 0.4.
Under this circumstance, the Meyer-Peter and Mller equation is sufficient. If this criteria is not met, then
a total load equation is necessary. Simons et al. (1981) developed a coarse grain total load transport
184




 Previous Page
Previous Page
