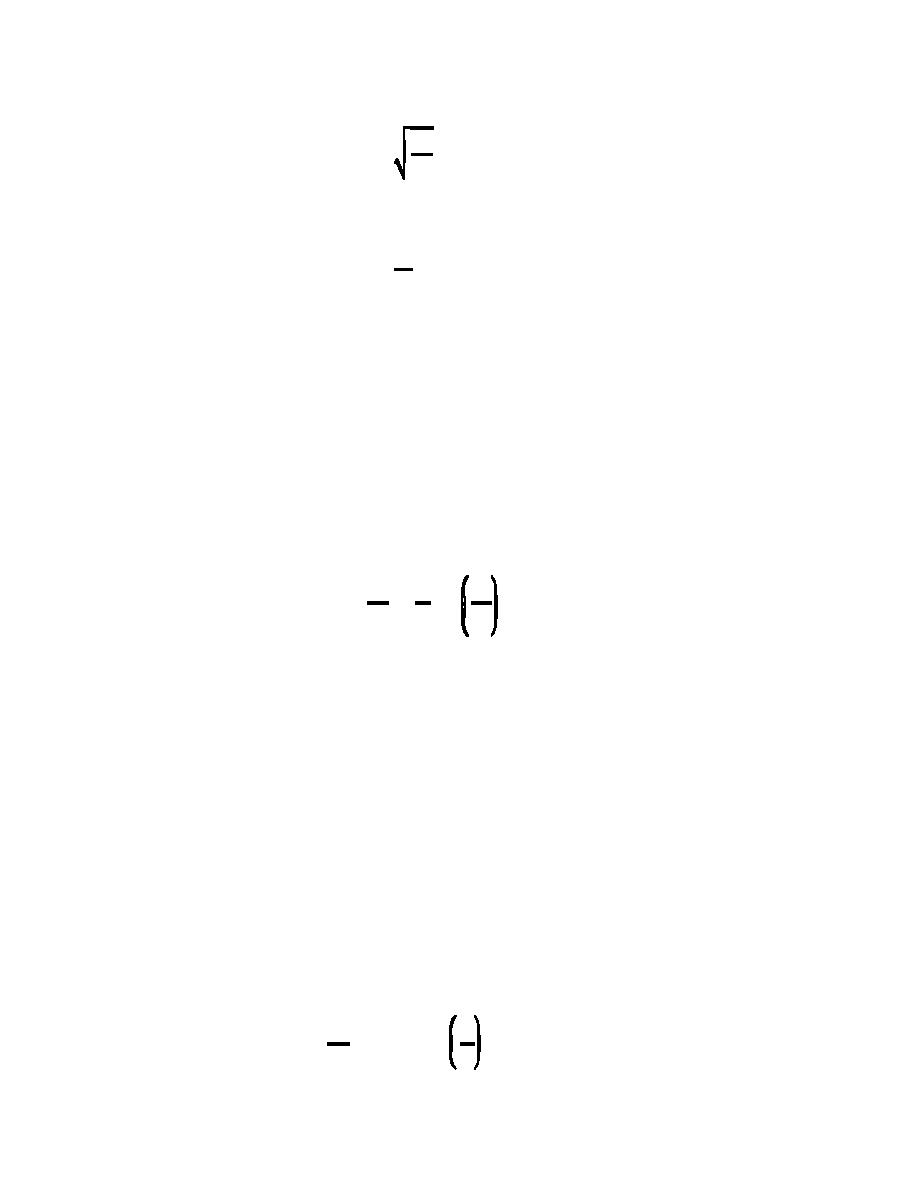
Fundamentals of Engineering Design
8g
(5.21)
@ R 1/2Sf1/2
V'
f
V ' C R 1/2S f1/2
(5.22)
N 2/3 1/2
V ' R Sf
n
(5.23)
where: V
=
cross section averaged velocity;
R
=
hydraulic radius;
Sf
=
friction slope; and
1 for metric units and 1.486 for English.
=
Sediment laden flows are typically characterized by turbulent velocity profiles. This is true for
gravel bed rivers in which there are more perturbations from rough boundaries. A turbulent velocity profile
was developed by Prandtl (1926) using the defined relationship between shear stress and velocity gradient.
In 1930, the velocity profile of Prandtl was verified by von Krmn. The velocity profile for turbulent flow
near a plane boundary known as the Prandtl-von Krmn universal velocity distribution is written as:
v
1
z
@ ln
'
(5.24)
u(
zo
6
where: v
=
velocity at a point in the vertical;
shear velocity, defined as (/)1/2;
u*
=
von Krmn constant ( . 0.4);
=
z
=
vertical distance from channel bottom;
zo
=
constant of integration;
=
shear stress; and
=
density.
Equation (5.24) applies to a no slip boundary (i.e., turbulent velocity components vanish near the
walls). This leads to viscous dominated flow in the location very near the boundary. The thin layer of
laminar motion is known as the laminar sublayer. For the condition where the roughness elements are
coarser than the laminar sublayer, the flow is termed hydraulically rough. Flow over gravel beds is
considered hydraulically rough. For rough planes it has been determined that zo./30, where is the
equivalent sand roughness from experiments by Nikuradse (1933). Integrating the Prandtl-von Krmn
universal velocity distribution over the channel depth, h, and transforming the relationship into base-10
logarithm yields the Keulegan (1938) equation:
V
h
' 5.75 @ log
% 6.25
(5.25)
u(
,
181




 Previous Page
Previous Page
